フェルミ推定は「筋道(論理)の構築」と「具体的数値の導入」が出来れば、正確な値を算出できます。詳細な説明については次の記事を参考にしてみてください。
今回は、最もオーソドックスな解法と人と差をつける?ひと手間かけた解法を紹介したいと思います。
目次
筋道(論理)の構築
まずは、結論に至るまでの筋道について考えましょう。もちろん、結論は今現在世界でトイレに入っている人の数です。それを数式で表すと次のようになります。
トイレに入っている人数=世界の人口×トイレに入っている時間/24
世界の人口もトイレに入っている時間も容易に計算できます。そのため、答えは簡単に算出できそうですね。しかし、この計算には一つ大きな問題があります。
それは、経度別による人口の偏りを考慮できていない点です。実際、アジア圏に人口はかなり偏っています。インドと中国だけで30億人近くになるわけですからね。人口の偏りを考慮しないと、昼夜のトイレ時間の違いを考慮することが出来ません。そりゃ、人は活動時間中にトイレにいきますからね。そうすると、より正確なトイレに入っている人数の推定が行えなくなってしまうわけです。
その点を考慮して立式すると、トイレに入っている人数は次のようになります。
トイレに入っている人数
=西経0~15度の範囲の人口×トイレに入っている時間/活動時間 or 活動時間外は0
+西経15~30度の範囲の人口×トイレに入っている時間/活動時間 or 活動時間外は0
+……………………………………………………………
+東経150~165度の範囲の人口×トイレに入っている時間/活動時間 or 活動時間外は0
+東経165~180度の範囲の人口×トイレに入っている時間/活動時間 or 活動時間外は0
となるわけです。この式だと、人口の偏りを考慮することができ、トイレに入っている人数の時間変化までも計算が可能になります。
具体的数値の導入
一般的な解法
偏りを考慮しない一般的な解法の場合は、次のような式で答えを求めることが出来ます。
トイレに入っている人数=世界の人口×トイレに入っている時間/24
世界の人口は約75億人です。そして、一日当たりの合計トイレ時間を10分とします。それらの値を代入すると、
トイレに入っている人数=75億×(1/6)/24≒0.52億
つまり、今現在5000万人ほどの人が世界中でトイレに入っていると考えられるわけです。
偏りを考慮した解法
人口の偏りを考慮する解法の場合は、考えるべきことが多くなります。流石に、経度15度ごとに人口分布は想像がつきませんので、アジア圏の人口と経度、アジア圏外の人口と経度を分けて考えます。
アジア圏の総人口は約45憶人です。そして、アジア圏の経度範囲は大体90度(45度~135度)ぐらいです。つまり、アジア圏外の人口は約30憶人、アジア圏外の経度範囲が270度となります。つまり、アジア圏の経度範囲では15度当たり7.5憶人となり、アジア圏外の経度範囲では15度当たり0.11億人となるわけですね。
そして、一日当たりのトイレ時間は10分とし、人の活動時間帯をは8時~0時とします。
これらのことを考慮して立式すると、
トイレに入っている人数
=1.7×(1/6)/16 or 活動時間外は0(西経165~180)
…..
+7.5×(1/6)/16 or 活動時間外は0(東経45~60)
…..
+7.5×(1/6)/16 or 活動時間外は0(東経120~135)
…..
+1.7×(1/6)/16 or 活動時間外は0(東経165~180)
となります。式で書いても少しわかりずらいので、エクセルでグラフ化したいと思います。なお、横軸の時間は世界標準時を基準としています。
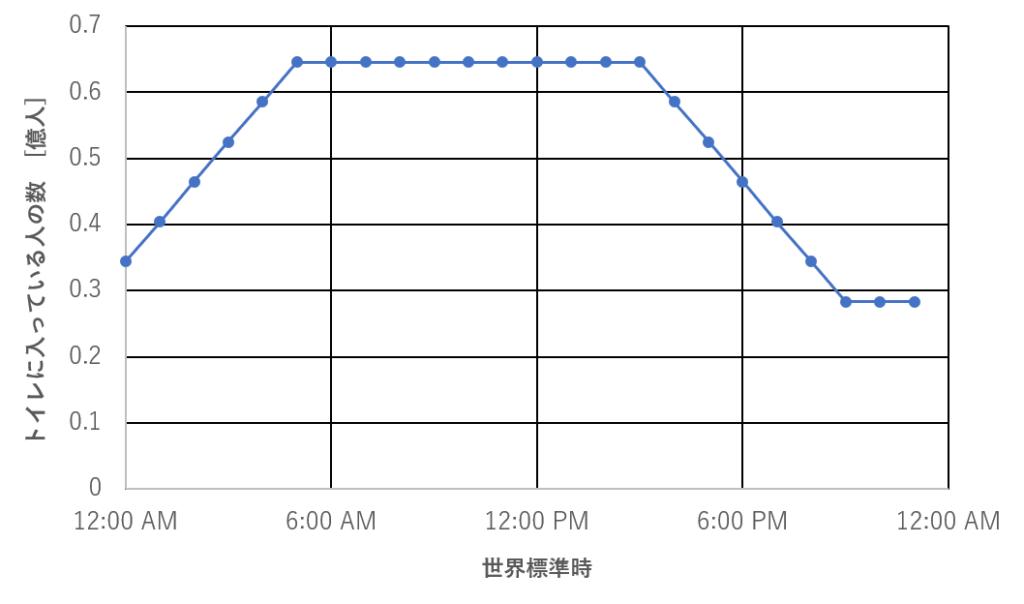
まとめ
今回の記事では、今現在世界にトイレに入っている人の数をフェルミ推定によって算出しました。そして、経度ごとの人口を考慮しないモデルと考慮するモデルの両方について考えてみました。2つのモデルを比較していただいたら、分かるように推定の精度を上げようと考えると、筋道(論理)の構築と具体的数値の導入がかなり大変になります。
そのため、考慮する・しないによって計算結果がどれくらい変化するのか?についてしっかり考える必要があります。大きく計算結果が変化するなら、多少計算過程がややこしくても考慮しなくてはなりません。
ちなみに、フェルミ推定は別名桁数推測(order estimation)と呼ばれています。つまり、桁数が合えばそれでいいわけです。そういった観点で考えると、今回の偏りを考慮したモデルは桁数を変える程ではありませんから、考慮しなくてよいという結論になりそうですね。
最近のコメント