最近、会社にて傘をパクられた「たま」です。しかも、ビニール傘じゃなくて16本足のしっかりとした傘をパクられました。周りにはビニール傘が沢山置いてあるのに…「会社には色んな人がいる」という諸先輩方の言葉が雨とともに身に沁みましたね…
もちろん、雨の中走って帰ったわけですが、その時ふと小さな頃の疑問を思い出しました。それは、雨の時「走る」と「歩く」ではどちらのほうが濡れないのか?という疑問です。というわけで、その疑問について考えてみました。
目次
問題の概要と軽い解説
まず、条件設定から始めていきます。それは、場所にかかわらず常に下方向に一定量の雨が降っていることです。そうじゃないと、一般化して考えられませんからね。
体が受ける雨の総量は上からの雨量+横からの雨量で表すことが出来ます。上からの雨量とは、頭上や肩に降り注ぐ雨のことです。横からの雨量とは、進行方向側の胴体に降り注ぐ雨(自ら当たりに行っている雨)のことです。車で例えるなら、バスのフロントガラスに相当します。
イメージとしてはこんな感じになります。赤矢印が上から降り注ぐ雨、オレンジ矢印が横から降り注ぐ雨(自ら当たりに行く雨)となっています。
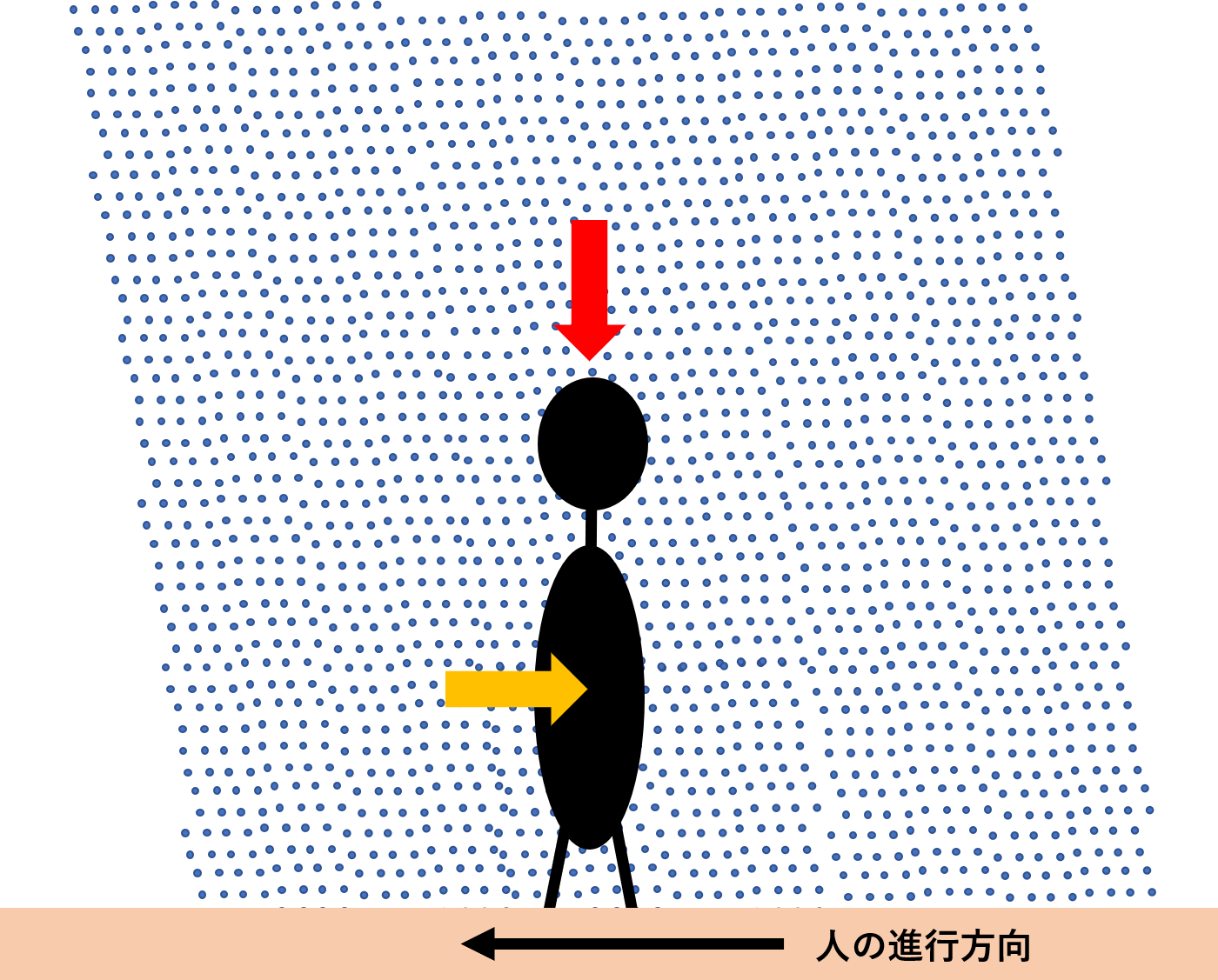
この図からも想像できるように、上からの雨は人の進行速度に依存しません。上から降る雨の総量は時間に依存します。もう少し詳しく説明すると、上からの総雨量=単位時間当たりの上から降る雨の量(一定)×目的地までの時間になります。そのため、中学生で習う一次関数で表すと、y=atという式になりますね。(y:上から降る雨の総量、a:単位時間当たりの上からの雨量、t:目的地までの時間)
一方で、横からの総雨量は一定になります。その理由は次の通りです。横からの総雨量=単位時間当たりの横から降る雨量×時間です。また、単位時間当たりの横から降る雨の量は進行速度に比例します。(バスのフロントガラスを想像してみるとわかりやすいと思います。)つまり、単位時間当たりの横から降る雨量=b×進行速度というわけです。そして、小学生習ったみはじの法則に則ると、進行速度=道のり/時間になります。そのため、横からの総雨量=b×進行速度×目的地までの時間=b×目的地までの道のりとなるわけです。道のりは定数なので、式で表すとy’=bc(y’:横から降る雨の総量、b=比例定数、c=道のり)また、y’が一定数になることは次の図を見ていただければ、容易に理解できると思います。
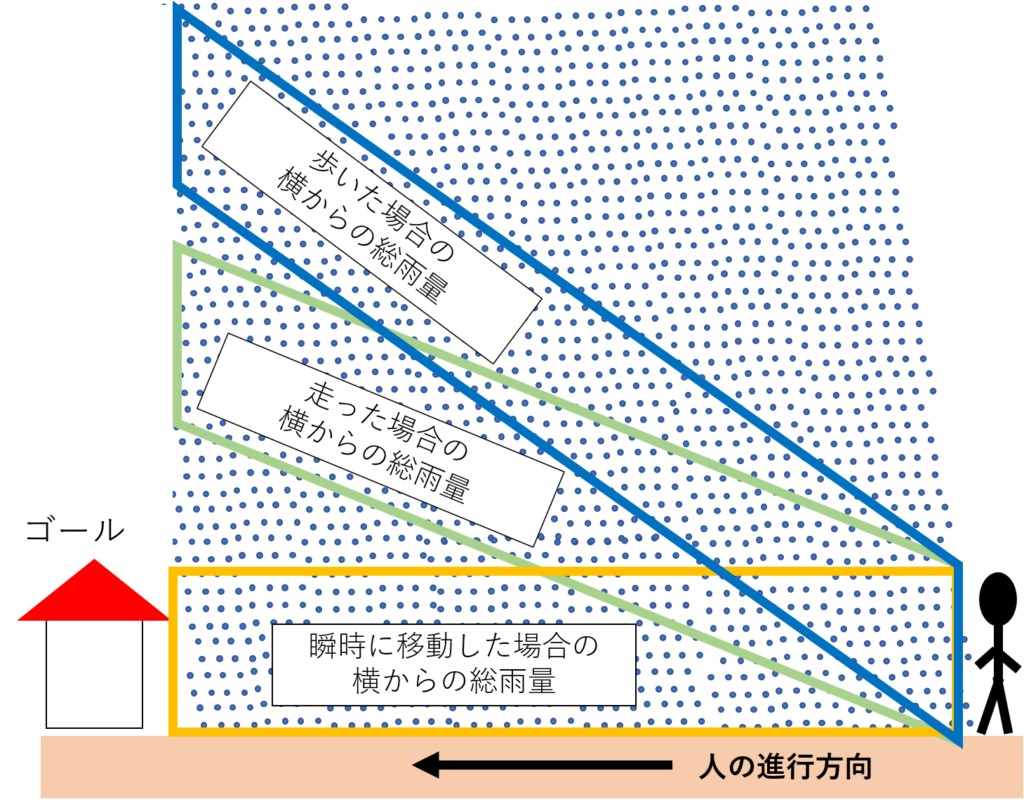
※平行四辺形の面積は底辺(人の身長)×高さ(目的地までの距離)で表せるので、黄色も緑色も青色も同じ面積になります。
これらのことから、体が受ける雨の総量はy+y’=at+bcとなり、時間に比例する一次関数であることが分かります。つまり、走る方が目的地に着くのが早くなるので、tが小さくなり体が受ける雨の総量は歩くよりも少なくなります。
中学数学風に証明してみると…
ここからは、数式を用いて証明風に解答を記述したいと思います。
仮定1:体が受ける雨の総量(Y)は、上からの雨量(y)+横からの雨量(y’)で表せるものとする。
仮定2:場所にかかわらず常に下方向に一定量の雨が降っているとする。
上からの雨量(y)は次のように表せる。
y=at…(1)
(a:単位時間当たりの上からの雨量, t:目的地までの時間)
次に、横からの雨量(y’)は次のように表せる。
y’=bvt…(2)
(b:比例定数, v:進行速度, t:目的地までの時間)
ここで、目的地までの道のりをcとすると、進行速度と時間の関係は次のように表される。
vt=c…(3)
(2)の式に(3)の式を代入すると、次のようになる。
y’=bc…(4)
これらのことから、体が受ける総雨量は次のように表される。
Y=y+y’=at+bc
よって、目的地までの時間tが小さくなる「走る」のほうが「歩く」よりも体が受ける総雨量は小さいと言える。
最後に
今回の結論は、「走る」ほうが「歩く」よりも雨に濡れないでした。しかし、これには考慮できていないものがあります。例えば、走る又は歩くことによる水はねや腕や足を振ることなどは考慮していません。例に挙げた二つは走った時のほうがより強く影響すると考えられます。そのため、結論が逆になる可能性も十分にあるわけです。
もしそうなった場合に注目すべきなのは仮定(前提)です。今回は「体が受ける雨の総量(Y)は、上からの雨量(y)+横からの雨量(y’)で表せるものとする。」という仮定(前提)をおきましたが、それが正しいことの保証はどこにもありません。つまり、「仮定が間違っていた。だから、結論も誤った」ということにもなり得るわけです。
実際、日常生活においても、無根拠な仮定(前提)というものは散見されます。そして、そういったものほど人が驚くような結論になっているケースが多いです。そういう時は、むやみに信じることなく、冷静に仮定と過程に問題がないかチェックするようにしましょう。そうすると、意外なところに穴があったりするものですよ…
最近のコメント