理系大学生の方なら、テイラー展開という言葉を一度は聞いたことがあると思います。この言葉を聞くだけで鳥肌が立つ人もいるのではないでしょうか?
私も学生時代には、このテイラー展開がよくわからず大学数学に躓いた記憶があります。そして、理解できないまま卒業しました…しかし、社会人になってテイラー展開を理解する必要が出てきました。
そして、テイラー展開の公式・意味・具体例について理解しました。というわけで、大学数学に躓きかけている理系大学生に向けてこの記事を書きたいと思います。できるだけ分かりやすく書いているので、頑張ってついてきてくださいね。
目次
テイラー展開の公式と意味
そもそも、テイラー展開にはどのような意味があるのか考えていましょう。とはいえ、以下のようなテイラー展開の公式を見せられても理解できないと思います。ただ、この式がn字の多項式であることはお分かりいただけると思います。
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ f^{(1)}(x_{0})\, (x-x_{0}) \\ &+\ \frac{1}{2\,!} f^{(2)}(x_{0})\, (x-x_{0})^2 \ \\ &+\ \frac{1}{3\,!} f^{(3)}(x_{0})\, (x-x_{0})^3\\ &\ \cdots \frac{1}{n\,!} f^{(n)}(x_{0})\end{align*}
この式の意味は、x0についての情報(f(x0)、f'(x0)、f”(x0)…)の値からその近傍にあるf(x)を求められるということです。つまり、直接的求められないf(x)の値を近傍の情報から間接的に求められるわけですね。
テイラー展開の具体例
二次関数の場合
例えば、f(x)=x2の場合、f(6)の値を知りたい時には、f(5)、f'(5)の情報があれば、次のように近似的に求めることが出来ます。

これを図解的に表すと、次のようになります。X=5の近傍において二つの線が近接していることが分かると思います。

複利計算の場合
例えば、100万円を年利0.3%の複利で20年間運用すると、お金はいくらになるか?を考えるとします。その場合の計算式は、1,000,000×(1.003)20となりますが、手計算では非常に時間がかかってしまいます。
ここでは、テイラー展開の公式を次のように用いています。

金利が0.003%なら100万円を20年4間運用しても、106万円にしかならないわけですね。ちなみに、この0.003%は預金金利の中では高い方です。なんだか悲しいですね…
【図解】公式の成り立ちを考える
テイラー展開の公式の成り立ちについて、図解的に理解を進めたいと思います。
今回題材とするのは、f(x)=x4の式です。先ほど触れたように、テイラー展開は多項式によってあらわされています。ここでは、f(2)、f'(2)などの情報からf(3)の値を算出したいと思います。
例えば、テイラー展開の式の先頭のみを取れば、定数ですので結果は次のようになります。このように、テーラー展開の式の先頭だけでは近い値を取ることが出来ません。
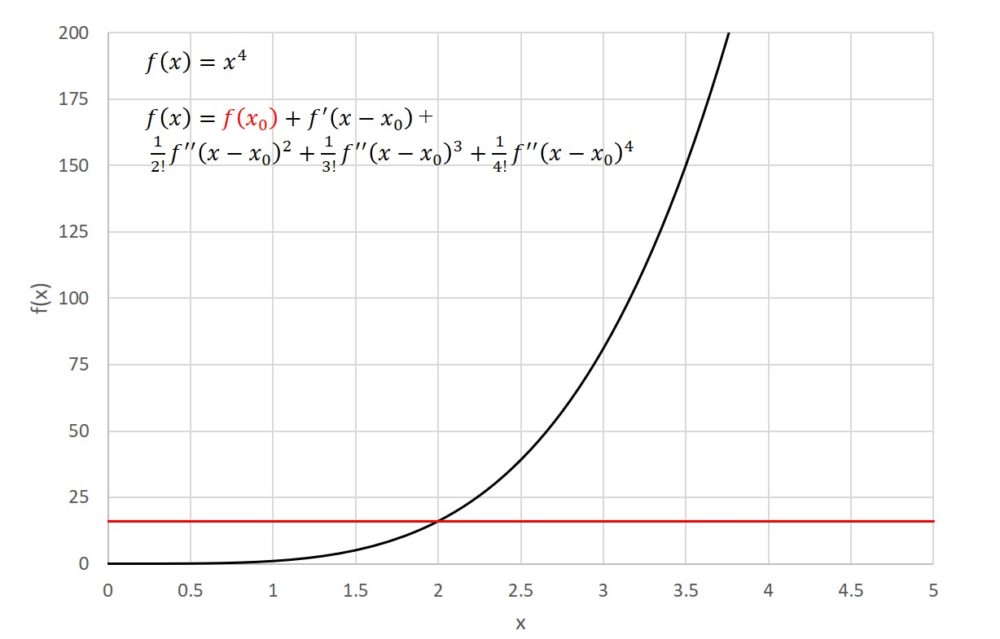
ですから、次に一次近似をしたいと思います。この問題における一次近似では、xの一乗を式に加えることを意味します。つまり、式は次のように表すことが出来ます。
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ k_{1}\, (x-x_{0})\end{align*}
ここで、両辺を一回微分すると次のようになります。
\begin{align*} f'(x) \ = k_{1}\end{align*}
この式を先ほどの式に代入すると、
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ f'(x_{0})\, (x-x_{0})\end{align*}
となり、一次の近似式を求めることができます。これをグラフで表すと次のようになります。X=2の近傍において、先ほどの近似式よりも精度良くなっていますね。
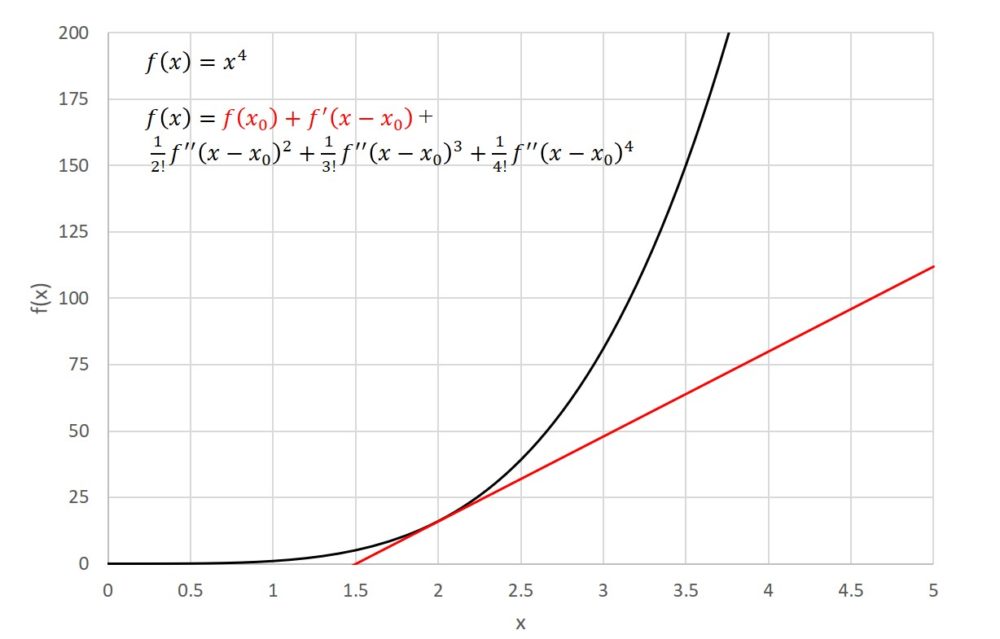
次に二次近似をしたいと思います。この問題における二次近似では、xの二乗を式に加えることを意味します。つまり、式は次のように表すことが出来ます。
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ f'(x)\, (x-x_{0})\\ &+ k_{2}(x-x_{0})^2 \ \end{align*}
ここで、両辺を一回微分すると次のようになります。
\begin{align*} f'(x) \ = \ f'(x)+2k_{2}(x-x_{0})\ \end{align*}
もう一度微分すると、
\begin{align*} f”(x) \ = 2k_{2}\end{align*}
この式を最初の式に代入すると、次のようになります。
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ f'(x_{0})\, (x-x_{0})\\ &+\ \frac{1}{2\,!} f”(x_{0})\, (x-x_{0})^2 \ \end{align*}
この式で近似すると、グラフは次のように変化します。先ほどよりもさらに精度が向上しています。二次近似ですので、近似式ももちろん二次方程式となります。
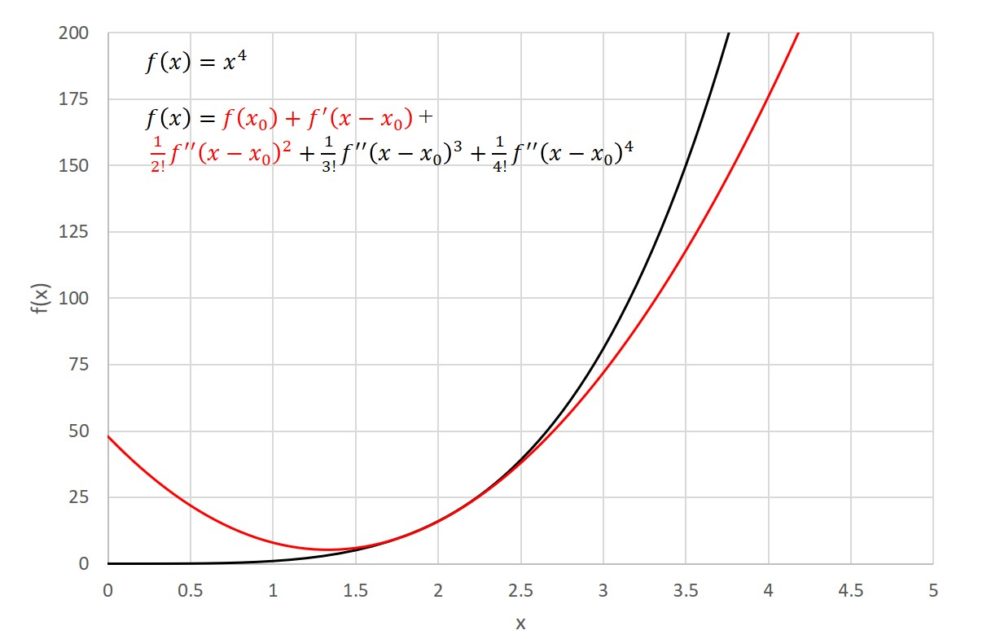
次も同様の手順で三次近似を行うと次のようになります。
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ f'(x)\, (x-x_{0})\\ &+\ \frac{1}{2\,!} f”(x_{0})\, (x-x_{0})^2\\ &+k_{3}(x-x_{0})^3 \ \end{align*}
一気に三回微分をすると、
\begin{align*}f^{(3)}(x)\ =3・2k_{3}\ \end{align*}
ですから、式は次のようになります。
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ f^{(1)}(x_{0})\, (x-x_{0}) \\ &+\ \frac{1}{2\,!} f^{(2)}(x_{0})\, (x-x_{0})^2 \ \\ &+\ \frac{1}{3\,!} f^{(3)}(x_{0})\, (x-x_{0})^3\end{align*}
この式をグラフで表すと次のようになります。かなり近づきましたね。
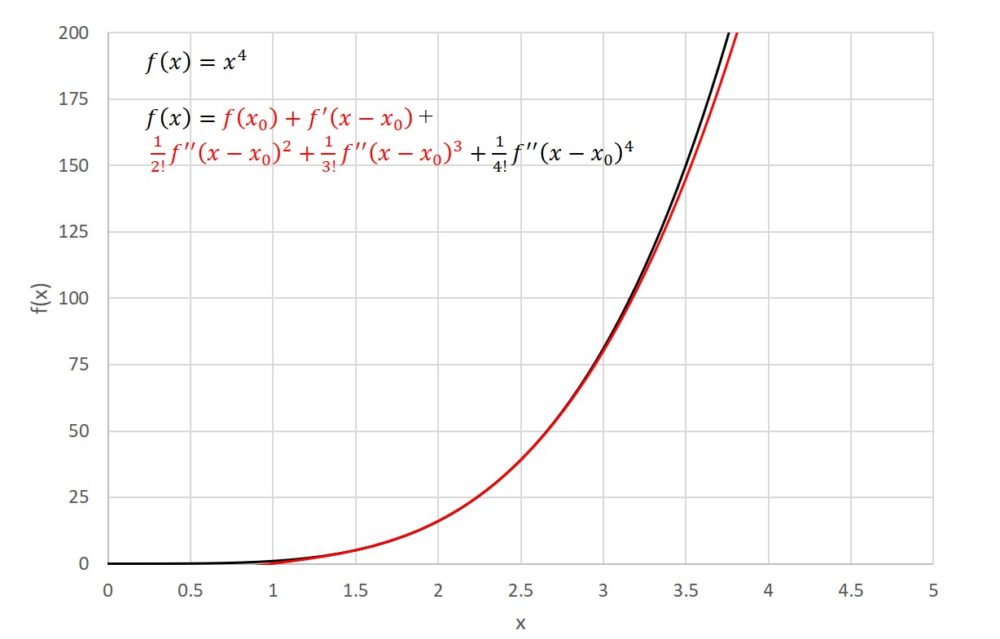
ちなみに、さらに4次近似を行うと、元の曲線と近似曲線が一致します。これは、4次関数に対して4次近似を行ったためです。右の式を展開すると左の式と完全に一致します。
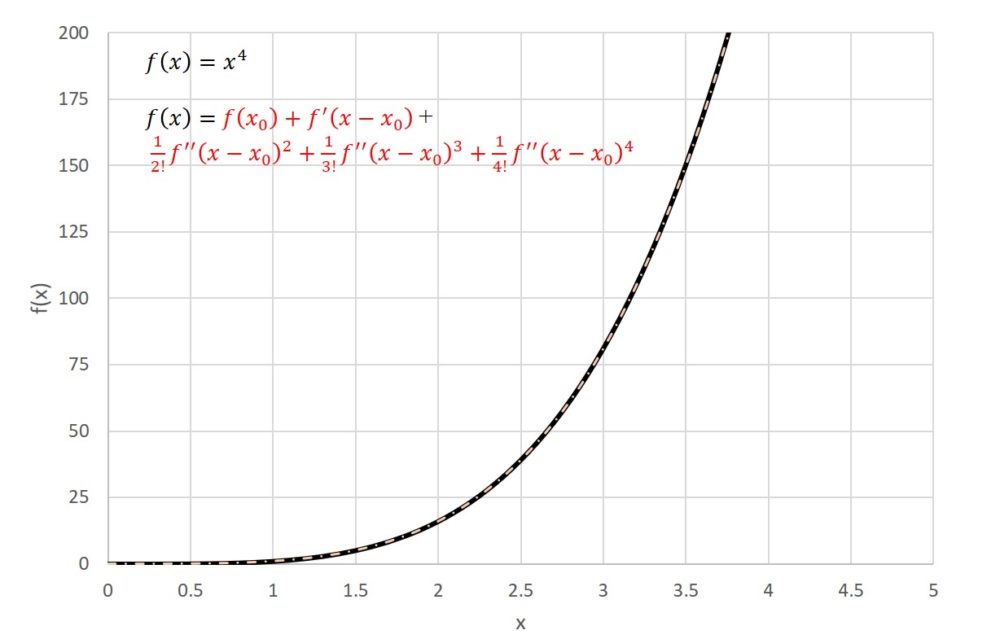
これをn回繰り返すと式は次のようになります。
\begin{align*} f(x) \ =\ f(x_{0}) \ &+\ f^{(1)}(x_{0})\, (x-x_{0}) \\ &+\ \frac{1}{2\,!} f^{(2)}(x_{0})\, (x-x_{0})^2 \ \\ &+\ \frac{1}{3\,!} f^{(3)}(x_{0})\, (x-x_{0})^3\\ &\ \cdots \frac{1}{n\,!} f^{(n)}(x_{0})\end{align*}
この式をΣ記号であらわすと次のようになります。
\begin{align*} f(x) \ =\sum_{n=0}^∞\frac{f^{n}(x_{0})}{n!}(x-x_{0})^{n}\end{align*}
これがテイラー展開の式となります。特に上のx0が0を取る時にはマクローリン展開の式になります。
\begin{align*} f(x) \ =\sum_{n=0}^∞\frac{f^{n}(0)}{n!}(x)^{n}\end{align*}
これらの式を用いれば、sinxやcosxなどの式も多項式によって表現することが出来るようになります。
最近のコメント